
Echantillonnage
Hervé BOEGLEN
![]() Introduction
et rappels de 1ère année
Introduction
et rappels de 1ère année
![]() Pourquoi échantillonner ?
Pourquoi échantillonner ?
Voici un schéma qui représente un système d'acquisition de données numérique :

A l'heure actuelle, notre environnement technologique utilise de plus en plus de systèmes numériques. Ces systèmes numérisent des informations analogiques, les traitent et les restituent dans notre monde physique. Les téléphones portables où les appareils photos numériques sont des exemples de tels systèmes.
Le système numérique doit être capable de transformer l'information analogique en une information numérique. Pour cela, il prend des échantillons sur le signal analogique continu à intervalle régulier (tous les te).
Il paraît évident que ces échantillons doivent représenter au mieux le signal analogique d'origine. Il est également indispensable de pouvoir reconstituer le signal analogique à partir des échantillons prélevés. C'est ce que nous allons voir dans la deuxième et troisième partie.
![]() La nécessité d'un nouvel outil mathématique
La nécessité d'un nouvel outil mathématique
Les systèmes numériques nécessitent l'emploi de processeurs spécialisés qui doivent être capables de stocker les informations numériques pour les traiter ou tout simplement les reconstituer... A première vue, on peut penser qu'il faut enregistrer tous les échantillons pour retrouver le signal analogique original. Autrement dit, si on a n échantillons, il faut une mémoire de n cases ! Si n tend vers l'infini, puisque le temps ne s'arrête pas, la mémoire doit disposer d'un nombre infini de cases !
Heureusement, M. Shannon est passé par là. Ainsi à l'aide d'un nombre limité d'échantillons, on va pouvoir écrire une relation mathématique qui permet avec des valeurs retardées du signal d'entrée et/ou du signal de sortie de déterminer un échantillon du signal de sortie à l'instant n puis l'instant d'après et ainsi de suite... Cette relation mathématique est appelée équation aux différences. Cependant, comme les équations différentielles pour les systèmes continus, les équations aux différences sont longues à résoudre dans le domaine temporel c'est pourquoi on utilise plus volontier un outil mathématique appelé transformée en z (cf. chapitre 2).
D'une approche qui se veut très simple, la transformée en z peut se déduire de la transformée de Fourier. Un signal analogique peut être représenté temporellement ou fréquenciellement. En connaissant ses composantes fréquencielles on peut reconstituer le signal analogique dans le domaine temporel par une transformation de Fourier inverse. Le seul problème est de discrétiser cette transformée de Fourier puisque notre signal est échantillonné ! Cette discrétisation nous amène à utiliser la transformée en z...
![]() De l'utilité des processeurs de traitement numérique du signal
(DSP)
De l'utilité des processeurs de traitement numérique du signal
(DSP)
On verra dans les chapitres suivants qu'on peut facilement créer une sinusoïde en partant d'une équation aux différences. On s'intéressera ensuite au filtrage des signaux en utilisant deux structures de filtres numériques : le filtre RIF et le filtre RII. La mise en application pratique se fera à l'aide de processeurs spécialisés appelés DSP (Digital Signal Processor). Leur intérêt est qu'ils sont optimisés pour les algorithmes de traitement de signal. Un DSP est, par exemple, capable d'exécuter une opération de multiplication-addition (très courante en traitement du signal) en un cycle d'horloge, alors que dans le cas cas d'un processeur classique, il faut dix cycles d'horloge. Autrement dit, un DSP cadencé à 40 Mhz équivaut à un processeur classique cadencé à 400 Mhz ! L'architecture d'un tel processeur sera vue dans le dernier cours.
![]() L'opération d'échantillonnage : approche intuitive
L'opération d'échantillonnage : approche intuitive
Rentrons dans le vif du sujet par un exemple : l'implémentation numérique d'un filtre de type passe-bas analogique de fonction de transfert :
H(w) = Y(w) / X(w) = 1 / (1 + jw/w0)
Vous avez vu en première année que le comportement d'un système est entièrement définit si on connait sa réponse impulsionnelle.
Dans ce cas, l'entrée x(t) du filtre étudiée est une impulsion de Dirac d(t). Pour rappel, la Transformée de Fourier de d(t), X(w) = 1. On obtient alors l'équation suivante :
H(w) = Y(w) = 1 / (1 + jw/w0)
Si l'on applique la Transformée de Fourier inverse à cette équation on obtient :
h(t) = w0 . exp(-w0*t) = 1/t0 . exp(-t/t0) avec to=1/w0
Il faut maintenant définir cette équation d'une manière utilisable par notre calculateur. On va alors prélever sur cette fonction h(t) cinq échantillons espacés de t0 seconde(s). La nouvelle fonction h(t) sera donc définie pour les instants 0.t0, 1.t0, 2.t0o, 3.t0o et 4.t0. On en déduit ses valeurs avec t0 = 1 s :
L'équation mathématique de h(t) échantillonnée, soit h*(t) s'écrit alors :
h*(t) = h0.d(t-0.t0) + h1.d(t-1.t0) + h2.d(t-2.t0) + h3.d(t-3.t0) + h4.d(t-4.t0)
Remarque : on suppose que la fonction exponentielle est définie jusqu'à 4.t0 puisqu'on est à 2% de sa valeur finale.
Nous pouvons maintenant appliquer la Transformée de Fourier à h*(t). Soit H*(w) la fonction de transfert de h*(t) :
H*(jw) = h0.exp(-jw0.t0) + h1.exp(-jw1.t0) + h2.exp(-jw2.t0) + h3.exp(-jw3.t0) + h4.exp(-jw4.t0)
Pour simplifier l'écriture, remplaçons exp(jwt0) par z. On obtient :
H(z) = h0.z-0 + h1.z-1 + h2.z-2 + h3.z-3 + h4.z-4
On peut alors écrire Y(z) :
Y(z) = H(z) . X(z) = [ h0.z-0 + h1.z-1 + h2.z-2 + h3.z-3 + h4.z-4] . X(z)
ou encore :
Y(z) = h0.z-0.X(z) + h1.z-1.X(z) + h2.z-2.X(z) + h3.z-3.X(z) + h4.z-4.X(z)
où z-k.X(z) représente l'entrée x(t) retardée de k.t0.
On peut alors en déduire l'équation aux différences suivante :
y(n) = h0.x(n) + h1.x(n-1) + h2.x(n-2) + h3.x(n-3) + h4.x(n-4)
Vérifions maintenant que cette équation aux différences nous permet bien d'obtenir la fonction h*(t) lorsque x(t) est une impulsion de Dirac.
Dans ce cas, on a x(0) = 1 et x(n) = 0 pour tout entier n positif et non nul. On obtient alors :
y(0) = h0.x0 = h0 = h(0)
y(1) = h0.x1 + h1.x0 = h1 = h(1)
y(2) = h0.x2 + h1.x1 + h2.x0 = h2 = h(2)
y(3) = h0.x3 + h1.x2 + h2.x1 + h3.x0 = h3 = h(3)
y(4) = h0.x4 + h1.x3 + h2.x2 + h3.x1 + h4.x0 = h4 = h(4)
On retrouve bien à la sortie du filtre passe-bas la réponse impulsionnelle h*(t) !
De manière plus synthétique, on peut écrire :

![]() L'opération d'échantillonnage : approche mathématique
L'opération d'échantillonnage : approche mathématique
Le processus d'échantillonnage est généralement décrit dans le domaine temporel. C'est une opération de base dans le domaine du traitement du signal numérique. Il permet, en effet, de convertir un signal analogique en une séquence d'échantillons qui sont généralement uniformément espacés en temps.
Plus précisément, il est nécessaire de choisir correctement la fréquence d'échantillonnage de manière à ce que la séquence d'échantillons prélevés définisse de manière unique le signal analogique d'origine.
Considérons un signal arbitraire g(t) défini quelque soit t. Si nous échantillonnons ce signal à une fréquence uniforme, c'est-à-dire que nous prenons un échantillon toutes les te secondes, nous obtenons une séquence infinie d'échantillons que l'on note {g(nte)}, où n est un entier naturel.

Soit gd(t) le signal obtenu si l'on multiplie la suite précédente par un peigne de dirac :
 (1)
(1)
A l'aide d'une table de Transformées de Fourier on obtient :
 (2)
(2)
L'équation ci-dessus montre que le processus d'échantillonnage d'un signal continu conduit à une représentation spectrale périodique de fréquence égale à la fréquence d'échantillonnage.
Une autre représentation fréquentielle du signal peut être obtenue en prenant la Transformée de Fourier de la première équation, on obtient alors :
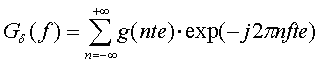 (3)
(3)
Cette relation est connue sous le nom de Transformée de Fourier à temps discret.
Les relations décrites précédemment s'appliquent de manière générale à tous les signaux g(t) de durée infinie. Supposons toutefois que le signal g(t) soit à bande passante limitée, c'est-à-dire qu'il ne contient aucune composante fréquentielle supérieure à B Hertz. Cela signifie que sa Transformée de Fourier G(f) est nulle pour |f| ³ B, comme le montre la figure suivante :

Si nous choisissons comme période d'échantillonnage te = 1/2B, alors le spectre Gd(f) de gd(t) pourra s'écrire :
 (4)
(4)

A partir de l'équation (2) on constate que la Transformée de Fourier de gd(t) peut aussi s'écrire :
 (5)
(5)
Ce qui dans les conditions suivantes :
1. G(f) = 0 pour |f| ³ B
2. fe = 2B
Nous permet d'obtenir :
 (6)
(6)
Si l'on remplace l'équation (4) dans l'équation (6) on obtient :
 (7)
(7)
En conséquence, si les échantillons de g(n/2B) d'un signal g(t) sont connues quelque soit t, alors sa Transformée de Fourier G(f) est déterminée de manière unique à l'aide la Transformée de Fourier à temps discret de l'équation (7). En d'autres termes, la séquence {g(n/2B)} possède toute l'information contenue dans g(t).
Considérons maintenant la reconstruction du signal g(t) à partir de la séquence d'échantillons {g(n/2B)}. Si l'on cherche la Transformée de Fourier inverse de l'équation (7), on peut écrire :
Si l'on intervertit l'ordre de la sommation et de l'intégration, on obtient :
 (8)
(8)
Soit :
(9)
L'équation précédente est une formule d'interpolation qui permet la reconstruction du signal g(t) à partir de la séquence {g(n/2B)} grâce à la fonction sinc(2Bt) qui joue le rôle d'une fonction d'interpolation. Chaque échantillon est multiplié par une version retardée de la fonction d'interpolation, et toutes les formes d'onde résultantes sont additionnées pour obtenir g(t).
Nous pouvons maintenant énoncer le théorème de l'échantillonnage pour des signaux à bande limitée de deux manières différentes :
1. Un signal à bande limitée, qui ne possède pas de composantes fréquentielles supérieures à B Hertz, est complètement décrit en précisant les valeurs du signal aux instants du temps séparés par 1/2B secondes.
2. Un signal à bande limitée, qui ne possède pas de composantes fréquentielles supérieures à B Hertz, peut être entièrement reconstitué à l'aide de ses échantillons pris à la fréquence de 2B échantillons par seconde.
La fréquence d'échantillonnage de 2B échantillons par seconde, pour un signal de largeur de bande de B Hertz est appelée fréquence de Nyquist, sa réciproque 1/2B (mesurée en secondes) est appelée intervalle de Nyquist.
Le théorème de l'échantillonnage est déterminé en supposant que le signal g(t) est à bande limitée. Ceci est rarement le cas en pratique, c'est pourquoi on est confronté au problème du sous-échantillonnage. En conséquence, le processus d'échantillonnage produit du repliement. Pour combattre les effets du repliement, on peut utiliser les deux méthodes suivantes :
1. Avant l'échantillonnage, on applique un filtrage passe-bas au signal g(t) pour atténuer les composantes hautes fréquences qui ne sont pas essentielles à l'information contenue dans le signal. On parle d'un filtre anti-repliement.
2. Le signal filtré est échantillonné à une fréquence plus élevée que la fréquence de Nyquist.
Remarquons que l'échantillonnage à une fréquence supérieure à la fréquence de Nyquist présente l'avantage de ne pas nécessiter la conception d'un filtre de reconstruction à flancs raides (difficilement réalisable en pratique car il se rapproche de la fonction rectangle).
L'applet JAVA ci-dessous illustre le théorème d'échantillonnage :
![]()
| Ó Hervé BOEGLEN, 2001 | |
| Dernières modifications le 08/10/2001 | |
| Pour toute remarque, contactez moi par email |



