
La transformée en Z
Hervé BOEGLEN
![]() 1. Définitions :
1. Définitions :
Soit x une fonction numérique supposée nulle sur R- et te un réel positif.

On appelle séquence numérique associée à x la suite des valeurs obtenues par échantillonnage de x selon la période te, on notera :
xe = {x(nte)}
fe est encore appelée fonction échantillonnée de x. x(nte) est l'échantillon de rang n.
On définit la suite retardée de mte par :
xret = {x(nte - mte)}
et la suite avancée par :
xav = {x(nte + mte)}
Exemples :
1. La suite échelon unité :
En supposant te = 1, elle est définie par :
u(n) = 1 pour tout n > 0
2. Suite de Dirac :
En supposant toujours te = 1, elle est définie par :
d(0) = 1, d(n) = 0 pour tout n.

![]() 1. Transformée en Z :
1. Transformée en Z :
On appelle transformée en z de la séquence numérique échantillonnant la fonction x, la fonction de la variable complexe z définie par :

![]() 2. Exemples de transformées :
2. Exemples de transformées :
2.1. Suite de Dirac :
On a :

Comme on a, x(n) = 1 à n = 0 seulement, on en déduit que :
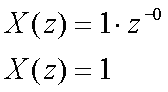
2.2. Suite échelon unité :
 Déterminer
la transformée en z de la suite échelon unité déterminée
par :
Déterminer
la transformée en z de la suite échelon unité déterminée
par :
u(n) = 1 pour tout n > 0.
2.3. Suite exponentielle :
 Déterminer
la transformée en z de la suite exponentielle déterminée
par :
Déterminer
la transformée en z de la suite exponentielle déterminée
par :
x(n) = an.u(n)
2.3. Table de transformées en z :


![]() 3. Domaine de convergence :
3. Domaine de convergence :
Le domaine de convergence de la transformée en z correspond au valeurs de z pour lesquelles X(z) est de valeur finie.
La transformée en z converge lorsque la serie réelle suivante converge :

Si l'on applique le critère de d'Alembert, on peut écrire :

Le critère impose que :

Soit :

En conclusion, la série converge à l'extérieur du cercle de centre origine et de rayon R.
Exemple :
La transformée en z de x(n) = an.u(n) :

converge pour |az-1| < 1, soit |z| > |a|. Son domaine de convergence est donc |z| > |a|.
4. Propriétés de la transformée en z :
4.1. Linéarité :
On peut montrer que la transformation en z est une opération linéaire :

4.2. Transformée en z d'une séquence décalée :
4.2.1. Séquence retardée x(n-m) :
On a :

En posant n-m = p, on obtient :

C'est-à-dire :

En particulier pour m = 1 :

La multiplication par z-1 correspond à un retard unité.
4.2.2. Séquence avancée x(n+m) :
On a :

En posant n+m = p, on obtient :

C'est-à-dire :

On retiendra plus particulièrement :

Remarque :
Il apparaît une analogie avec les résultats obtenus dans l'étude des transformées de Laplace et de Fourier.
L'avance (respectivement la dérivation) se traduit par la multiplication par z (respectivement par s ou j2pf).
Le retard (respectivement l'intégration) se traduit par la division par z (respectivement par s ou j2pf).
4.3. Multiplication par une exponentielle :

C'est-à-dire :
![]()
4.4. Produit de convolution :
Par analogie avec le produit de convolution de deux fonctions intégrables, on définit le produit de convolution de deux séquences numériques par :

La transformée en z de ce produit de convolution s'écrit :

En posant n-k = m et en conservant m et k comme indices de sommation, il vient :

Les sommations étant indépendantes :
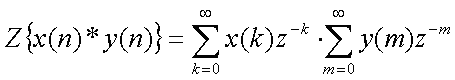
C'est-à dire :
![]()
 Calculer
la transformée en z du produit de convolution des séquences
suivantes :
Calculer
la transformée en z du produit de convolution des séquences
suivantes :
x(n) = 2anu(n) et y(n) = d(n-1)
5. Transformée en Z inverse :
La méthode consiste à se servir d'une table de transformées en z. Cependant, il est rare que l'on soit en présence de transformées élémentaires. Souvent le résultat se présente sous la forme d'une fraction rationnelle qu'il faudra décomposer en éléments simples. C'est ce que montre l'exercice suivant :
 Déterminer
la transformée inverse de :
Déterminer
la transformée inverse de :

6. Applications :
6.1. Résolution d'équations aux différences :
Les systèmes discrets sont souvent représentés sous la forme d'une équation aux différences. Cette équation donne la sortie du système en fonction des échantillons présent et passés du signal d'entrée ainsi que des échantillons précédents de la sortie.
Voici un exemple d'équation aux différences :
y(n) = 2y(n-1) + 3x(n) -2x(n-2)
Dans le cas général, on peut écrire :

Ce qui s'écrit en appliquant la transformée en z :

On voit qu'il est possible de déterminer la transformée en z d'une équation aux différences, de manipuler cette transformée puis d'appliquer la transformation inverse pour finalement obtenir la solution de l'équation aux différences dans le domaine temporel.
 Résoudre
à l'aide de la transformée en z, l'équation aux différences
suivante :
Résoudre
à l'aide de la transformée en z, l'équation aux différences
suivante :
y(n) - ay(n-1) = u(n)
6.2. Fonctions de transfert :
On vient de voir que la relation entrée-sortie d'un système pouvait être représentée par :

Or, on peut également l'écrire sous la forme suivante :

Soit :

H(z) représente la fonction de transfert du système et on a donc Y(z) = H(z)X(z). Si l'entrée X(z) est une impulsion de Dirac alors, Y(z) = H(z). On sait également que si l'on connait la réponse impulsionnelle d'un système son comportement est entièrement déterminé. En conséquence, la connaissance de la fonction de transfert H(z), permettra de déduire la réponse du système à une entrée quelconque.
On peut donc représenter un système des deux façons équivalentes suivantes :

6.3. Réponse en fréquence :
La réponse en fréquence d'un signal discret h(k), est donnée par :

En d'autres termes, la réponse en fréquence peut être obtenue à partir de la fonction de transfert H(z) en remplaçant z par ejq.
 Déterminer
la réponse en fréquence de la fonction de transfert suivante
:
Déterminer
la réponse en fréquence de la fonction de transfert suivante
:

6.4. Conception de filtres numériques :
Ce sujet est immense, il fera donc l'objet des deux chapitres suivants.
![]()
| Ó Hervé BOEGLEN, 2001 | |
| Dernières modifications le 08/10/2001 | |
| Pour toute remarque, contactez moi par email |


