
Les filtres numériques RIF
Hervé BOEGLEN
![]() 1. Rappels :
1. Rappels :
![]() Le signal de sortie y(t) de tout filtre analogique est un produit de convolution
entre sa réponse impulsionnelle h(t) et le signal d’entrée
x(t) :
Le signal de sortie y(t) de tout filtre analogique est un produit de convolution
entre sa réponse impulsionnelle h(t) et le signal d’entrée
x(t) :

Cette relation temporelle s'exprime plus simplement dans le domaine fréquentiel sous la forme :
Y(f) = H(f).X(f)
H(f) = Y(f)/X(f) est appelée la fonction de transfert du filtre.

![]() La
conception d'un filtre numérique impose de fixer un certain nombre
de paramètres :
La
conception d'un filtre numérique impose de fixer un certain nombre
de paramètres :

![]() 2. Le filtre numérique à
Réponse Impulsionnelle Finie (RIF):
2. Le filtre numérique à
Réponse Impulsionnelle Finie (RIF):
2.1. Définition :
Il s'agit d'une simple transposition de l'équation du produit de convolution en temps continu dans le domaine du temps échantillonné. Son équation générale s'écrit :

Un filtre RIF peut également être représenté par un graphe :

Exemple :
Un filtre FIR est entièrement déterminé si l'on connait l'ensemble des coefficients h. Par exemple si :
h(k) = {3, -1, 2, 1}
alors on peut écrire que :

2.2. Comment le filtrage RIF affecte-t-il le signal d'entrée ?
Soit le signal suivant :


Nous allons lui appliquer un filtrage à l'aide du filtre RIF définit par :
h(k) = {1/7, 1/7, 1/7, 1/7, 1/7, 1/7, 1/7}
Ce filtre est appelé filtre moyenneur à 7 points.
On obtient alors :

On constate que le filtre a atténué les variations du signal d'entrée et qu'il introduit un décalage de 3 échantillons du signal de sortie.
2.3. Comment calcule-t-on un produit de convolution numérique ?
L'équation générale du filtre FIR montre que pour obtenir le signal y(n) il faut convoluer les séquences x(n) et h(n). Pour des séquences de longueur finie on peut utiliser l'algorithme mis en oeuvre dans l'exemple qui suit.
Soit à convoluer les deux séquences suivantes :
x(n) = {2, 4, 6, 4, 2} et h(n) = {3, -1, 2, 1}
On a :
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| x(n) | 2 | 4 | 6 | 4 | 2 | ||||
| h(n) | 3 | -1 | 2 | 1 | |||||
| h(0)x(n-0) | 6 | 12 | 18 | 12 | 6 | ||||
| h(1)x(n-1) | -2 | -4 | -6 | -4 | -2 | ||||
| h(2)x(n-2) | 4 | 8 | 12 | 8 | 4 | ||||
| h(3)x(n-3) | 2 | 4 | 6 | 4 | 2 | ||||
| y(n) | 6 | 10 | 18 | 16 | 18 | 12 | 8 | 2 |
La justification de cet algorithme devient évidente si on écrit y(n) :
y(n) = h(0)x(n) + h(1)x(n-1) + h(2)x(n-2) + ...
2.4. Pourquoi parle-t-on de réponse impulsionnelle finie ?
Répondons à cette question en abordant le cas pratique de la conception d'un filtre numérique passe-bas idéal :
Sa fonction de transfert est donnée par :

La table des transformées de Fourier, nous permet d'en déduire la réponse impulsionnelle h(t) :


On constate, toutefois, que h(t) n'est pas causale (elle existe avant t = 0), nous la décalons suffisamment pour que h’(t) = h(t-td) » 0 pour tout t < 0. On obtient finalement :

Soit :
h'(t) = 2fc.sinc(2fc(t-td))
Maintenant il s'agit de prendre M échantillons sur la réponse impulsionnelle h'(t) pour obtenir la réponse impulsionnelle échantillonnée he(t) :

On constate sur ce dernier graphe que he(t) n'existe qu'aux instants mTe et que td = (M-1)/2. On peut donc écrire :
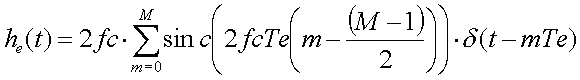
Conséquence de l'échantillonnage sur la fonction de transfert H(f) :
D'après l'équation (2) du chapitre 1, on obtient :

On constate que He(f) est périodique de période Te et qu'elle est multipliée par la constante fe.
Finalement, on obtient les coefficients h(m) qui sont donnés par :

 Calculer
les coefficients h(m) d'un filtre passe-bas idéal dont fc = 100Hz,
fe = 500Hz et M = 15. A l'aide de MATLAB, afficher la sortie du filtre y(n)
si x(n) = sin(2p50nTe)
+ sin(2p200nTe).
Calculer
les coefficients h(m) d'un filtre passe-bas idéal dont fc = 100Hz,
fe = 500Hz et M = 15. A l'aide de MATLAB, afficher la sortie du filtre y(n)
si x(n) = sin(2p50nTe)
+ sin(2p200nTe).
2.5. Qu'est-ce que le fenêtrage ?
Pour répondre à cette question, il suffit d'étudier les conséquences de la troncature de la réponse impulsionnelle. Reprenons le cas de l'exercice précédent ou M = 15 et cherchons H(f) en calculant la transformée de Fourier de he(t). Après quelques lignes de calcul on obtient :


On constate que la fonction de transfert obtenue est différente de la fonction souhaitée. On observe un phénomène d’oscillations analogue au phénomène de Gibbs du domaine continu.
Pour atténuer ces ondulations et/ou se rapprocher de la fonction de transfert théorique, on a recours au fenêtrage.
Principe :

Dans l'exemple précédent, nous n'avons pas modifié les coefficients puisque nous avons utilisé une fenêtre rectangulaire.
IL existe un grand nombre de fenêtres ayant chacune leur spécificité. On pourra les visualiser à l'aide de la fonction MATLAB window.
Exemple :
Fenêtre de Hamming :
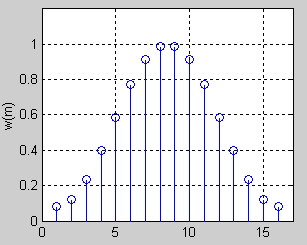
On a pour cette fenêtre :
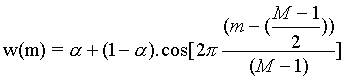
Conséquence de l'application de la fenêtre de Hamming sur la fonction de transfert du filtre passe-bas précédent :
Les nouveaux coefficients de la réponse impulsionnelle hn(mTe) ont été calculés de la façon suivante :
hn(mTe) = h(mTe).w(mTe)

2.6. Conclusion :
Les filtres RIF sont d’une synthèse relativement simple par rapport aux performances du filtre désiré. Ils possèdent une phase linéaire.
L’inconvénient majeur étant,
pour une précision donnée, un nombre de coefficients élevé
nécessitant un temps de calcul élevé donc une fréquence
d’échantillonnage assez faible.
![]()
| Ó Hervé BOEGLEN, 2001 | |
| Dernières modifications le 08/10/2001 | |
| Pour toute remarque, contactez moi par email |
