
Les filtres numériques RII
Hervé BOEGLEN
![]() 1. Définition :
1. Définition :
On appelle filtre RII, un filtre numérique défini par l'équation suivante :
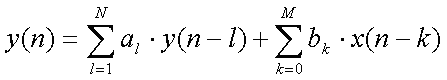
On remarque que cette équation fait intervenir non seulement les échantillons retardés du signal d'entrée mais également les échantillons retardés du signal de sortie. On parle également de filtre récursif.
![]() 2. Conception d'un filtre RII
:
2. Conception d'un filtre RII
:
Contrairement aux filtres RIF on ne part pas de la réponse impulsionnelle théorique d'un filtre analogique que l'on tronque mais directement de la fonction de transfert en s du filtre analogique. Cette fonction de transfert analogique n'étant pas tronquée, sa réponse impulsionnelle est entièrement conservée, c'est pourquoi on parle de filtre à réponse impulsionnelle infinie.
Il existe plusieurs méthodes pour passer de la fonction de transfert en s à la fonction de transfert en z, non ne décrirons cependant que la méthode de la transformation bilinéaire.
Dans ce cas, on a l'égalité suivante :
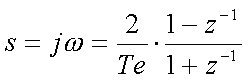
Cette méthode présente toutefois l'inconvénient que la pulsation dans le domaine échantillonné subit, de par le fait de cette transformation non linéaire, une distorsion et ne correspond plus tout à fait à la pulsation du domaine analogique. On a en effet :
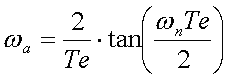
2.1. Mode opératoire pour la conception d'un filtre numérique RII :
1. A partir du gabarit de filtrage, détermination d'une fonction d'approximation
2. Détermination de l'ordre du filtre
3. Utilisation d'un polynome normalisé à partir d'une table
4. Dénormalisation
5. Appliquer la transformation bilinéaire
6. Correction de la fréquence analogique
7. Déduire les équations de récurrence
8. Implantation sur calculateur
 Soit
à déterminer l'équation caractéristique discrète
du filtre de Butterworth d'ordre 2, passe bas et de fc = 50Hz. La période
d'échantillonnage Te est de 1ms. La table des polynomes de Butterworth
donne :
Soit
à déterminer l'équation caractéristique discrète
du filtre de Butterworth d'ordre 2, passe bas et de fc = 50Hz. La période
d'échantillonnage Te est de 1ms. La table des polynomes de Butterworth
donne :
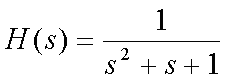
2.2. Condition
de stabilité d'un filtre RII :
En utilisant la transformée en z, la relation E/S d'un filtre RII peut s'écrire :
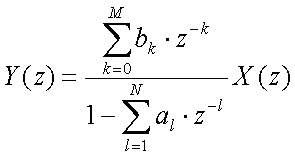
On remarque que si le dénominateur est égal à zéro, le système devient instable. Il faut donc s'assurer de ne jamais se trouver dans cette éventualité. Pour étudier la stabililité du système, on montre que la fonction de transfert d'un filtre RII d'ordre quelconque peut se mettre sous la forme suivante :
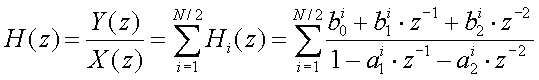
Il suffit alors de s'assurer de la stabilité de chacune des sections d'ordre 2 pour être certain de la stabilité du système.
Un filtre RII d'ordre 2 est stable si les racines du dénominateur de sa fonction de transfert possèdent un module inférieur à 1 :
Le dénominateur est égal à :
1 - a1z-1 + a2z-2
Les racines de ce trinôme s'écrivent :
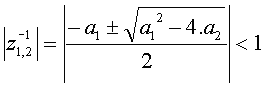
Ce qui conduit aux conditions suivantes :
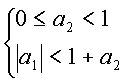
2.3. Les différentes structures de réalisation :
Il existe différentes structures permettant d'implémenter les filtres RII sur un calculateur. En voici deux exemples :
2.3.1. Structure directe canonique de type 1 :

2.3.2. Structure directe canonique de type 2 :
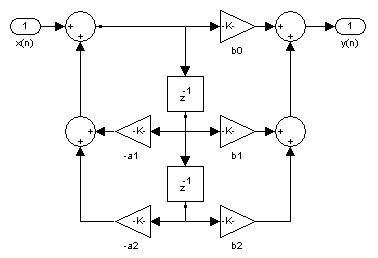
Remarquons que la structure canonique directe de type 2 nécessite moins de cellules mémoire que la structure canonique directe de type 1.
![]()
| Ó Hervé BOEGLEN, 2001 | |
| Dernières modifications le 08/10/2001 | |
| Pour toute remarque, contactez moi par email |
