
La transformée de Fourier rapide
Hervé BOEGLEN
![]() 1. La Transformée de Fourier Discrète
:
1. La Transformée de Fourier Discrète
:
Nous avons vu dans le chapitre 1 que l'expression de la Transformée de Fourier à Temps Discret s'écrivait :

Cette série comporte un nombre infini de termes et n'est donc pas exploitable directement sur un calculateur. C'est pourquoi on introduit la notion de Transformée de Fourier Discrète. Son calcul est limité à un nombre fini de valeurs de n et à un nombre fini de valeurs de f. Son intérêt pratique est très largement dû à la découverte d'un algorithme de calcul rapide connu sous le nom de Transformée de Fourier Rapide (TFR) ou Fast Fourier Transform (FFT) en anglais.
Si l'on se limite à N valeurs pour n et L valeurs pour f en posant que f = k/L, on peut écrire :

On prend souvent L = N, mais ce n'est pas systématique. En fait L influe sur la précision du tracé du spectre et N sur la résolution en fréquence. Il est d'usage de poser WN = e-j2p/N, on obtient alors :

![]() 2. La Transformée de Fourier
Rapide :
2. La Transformée de Fourier
Rapide :
La Transformée de Fourier Discrète est une méthode très efficace pour déterminer le spectre de n'importe quel signal. Son seul inconvénient est le temps de calcul qu'elle nécessite. En effet, il faut faire évoluer les deux indices k et n de 0 à N ce qui implique N2 opérations. Ainsi une TFD calculée sur N = 1000 points nécessiterait 106 cycles machine. Même sur un DSP (pourtant optimisé pour ce type d'opération), ayant un temps de cycle de 50ns cela prendrait 50ms, soit une fréquence fe de 20Hz !
L'intérêt d'un algorithme de FFT est de réduire sensiblement ce temps de calcul. Voyons maintenant les détails de son implémentation. Précisons que cet algorithme est à son efficacité maximale si N = 2p. Si le nombre d'échantillons sur x(n) n'est pas en puissance de 2, il faudra alors le compléter avec des zéros (zero padding en anglais) de façon à obtenir cette condition.
La première étape consiste à réduire le signal d'entrée x(n) en séquences plus petites, on parle alors de décimation en temps :
A partir de :

on peut écrire :

soit :

En revenant à la définition de WN :
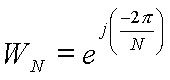
on remarque que :

Finalement :

On constate que la TFD de X(k) peut s'écrire sous la forme de deux TFD plus petites de longueur N/2. Quel intérêt ? Et bien si N = 1000, le calcul prendra 5002 + 5002 + 500 = 50500 opérations plutôt que 106 ! De plus, en supposant que N est une puissance de 2, on peut répéter le processus jusqu'à obtenir une somme de TFD de base 2. On peut montrer que le nombre d'opérations nécessaires devient alors égal à Nlog2(N).
Pour mieux appréhender les subtilités de cet algorithme, prenons N = 4 :
En remarquant que :

on peut écrire :
![]()
Pour toutes les valeurs de k, on obtient :

après avoir remarqué que :

et que :

Il est souvent plus aisé de visualiser les opérations sur un graphe, tel que celui de la figure suivante :

Ce graphe illustre l'une des caractéristiques essentielles de la FFT : le papillon. Chaque étape est constituée de plusieurs papillons élémentaires comme celui de la figure suivante :

![]() 3. La Transformée de Fourier Rapide sous MATLAB
:
3. La Transformée de Fourier Rapide sous MATLAB
:
Sous MATLAB, la FFT est une fonction interne (built-in) :
FFT(X,N) is the N-point FFT, padded with zeros if X has less than N points and truncated if it has more.
 Tracer
le spectre d'un signal carré de fréquence 1KHz, centré,
de rapport cyclique égal à 50% et d'amplitude maximale 1V
à l'aide de la fonction fft de MATLAB.
Tracer
le spectre d'un signal carré de fréquence 1KHz, centré,
de rapport cyclique égal à 50% et d'amplitude maximale 1V
à l'aide de la fonction fft de MATLAB.
![]()
| Ó Hervé BOEGLEN, 2001 | |
| Dernières modifications le 08/10/2001 | |
| Pour toute remarque, contactez moi par email |


