
Notions de filtrage adaptatif
Hervé BOEGLEN
L'aspect mathématique du filtrage adaptatif est basé sur les travaux du célèbre mathématicien Allemand du 19ème siècle GAUSS. Celui-ci a étudié la théorie de la minimisation des moindres carrés. Cette théorie est largement utilisée aujourd'hui dans tous les domaines de la science et de la technologie. Les DSP ont rendu possible l'utilisation de cette théorie en temps réel sur des signaux échantillonnés jusque environ 100kHz.
L'une des premières utilisations proposée en traitement adaptatif numérique du signal a été la publication de WIDROW et HOFF concernant des circuits de commutations adaptatifs en 1960. Ces travaux ont suscité beaucoup d'intérêt et on été complétés par d'autres publications dans les années 1970.
Le traitement adaptatif du signal a depuis trouvé de nombreuses applications. On peut les classer dans les catégories suivantes :
- détection de signaux (le signal x est-il présent ?),
- estimation de signaux (qu'est-ce que c'est ?),
- estimation d'un paramètre ou d'un état,
- compression de signaux,
- synthèse de signaux,
- etc.
![]() Architecture
d'un processeur de traitement adaptatif du signal :
Architecture
d'un processeur de traitement adaptatif du signal :

La sortie y(k) du filtre adaptatif est égal au produit de convolution entre le signal d'entré x(k) et le vecteur w(k) représentant les coefficients du filtre adaptatif. Le vecteur w(k) est mis à jour selon une fonction basée sur le signal d'erreur e(k). A chaque instant k, un vecteur w(k + 1) est créé pour l'instant suivant. Cet algorithme adaptatif est implémenté dans le but de filtrer x(k) de façon à ce que y(k) soit le plus proche possible du signal désiré d(k), ceci en minimisant le carré du signal d'erreur e(k) = d(k) - y(k).
Le filtre adaptatif peut être de type RIF ou RII. Toutefois, la structure la plus utilisée est le RIF. L'algorithme utilisé peut être basé sur les moindres carrés (LMS) ou les moindres carrés récursifs (RLS). Chaque algorithme possède des caractéristiques particulières en terme d'erreur minimale atteignable, temps de convergence et stabilité.
En général, on distingue quatre types d'architectures de filtres adaptatifs :
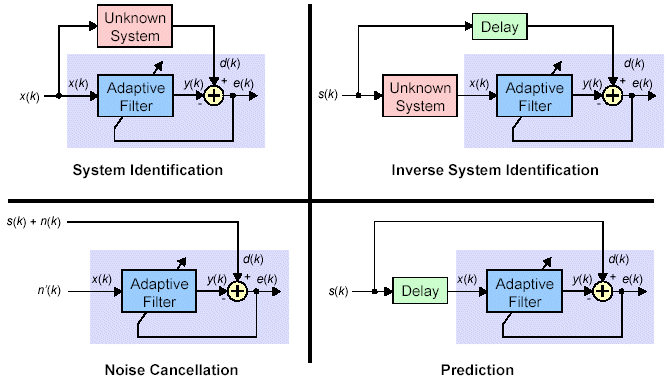
![]() Identification de système : si l'erreur
obtenue est nulle alors les coefficients de la fonction de transfert du
filtre adaptatif sont identiques à ceux de la fonction de transfert
du système inconnu.
Identification de système : si l'erreur
obtenue est nulle alors les coefficients de la fonction de transfert du
filtre adaptatif sont identiques à ceux de la fonction de transfert
du système inconnu.
![]() Identification de l'inverse d'un système : de la même
manière que précédemment si l'erreur obtenue est nulle
alors les coefficients de la fonction de transfert du filtre adaptatif sont
identiques à ceux de l'inverse de la fonction de transfert du système
inconnu. Le délai est nécessaire pour rendre le système
causal.
Identification de l'inverse d'un système : de la même
manière que précédemment si l'erreur obtenue est nulle
alors les coefficients de la fonction de transfert du filtre adaptatif sont
identiques à ceux de l'inverse de la fonction de transfert du système
inconnu. Le délai est nécessaire pour rendre le système
causal.
![]() Suppression de bruit : dans ce système
on utilise un bruit n'(k) corrélé avec le bruit n(k) à
éliminer. Dans ce cas, le filtre adapte ses coefficients pour que
l'on obtiennne e(k) » s(k).
Suppression de bruit : dans ce système
on utilise un bruit n'(k) corrélé avec le bruit n(k) à
éliminer. Dans ce cas, le filtre adapte ses coefficients pour que
l'on obtiennne e(k) » s(k).
![]() Filtre prédictif
: dans ce cas si l'erreur tend vers 0 alors le filtre peut prévoir
les échantillons futurs du signal s(k) qui sont basés sur
les observations précédentes. Ceci peut fonctionner sur des
signaux périodiques. L'une des applications est l'extraction de signaux
noyés dans le bruit. On peut également utiliser ce système
pour atténuer les variations d'un signal, mais c'est une application
impossible à réaliser en temps réel.
Filtre prédictif
: dans ce cas si l'erreur tend vers 0 alors le filtre peut prévoir
les échantillons futurs du signal s(k) qui sont basés sur
les observations précédentes. Ceci peut fonctionner sur des
signaux périodiques. L'une des applications est l'extraction de signaux
noyés dans le bruit. On peut également utiliser ce système
pour atténuer les variations d'un signal, mais c'est une application
impossible à réaliser en temps réel.
![]()
| Ó Hervé BOEGLEN, 2001 | |
| Dernières modifications le 08/10/2001 | |
| Pour toute remarque, contactez moi par email |