
Conception de filtres RIF
Hervé BOEGLEN
![]() Les
bases :
Les
bases :
Les paramètres importants d'un filtre numérique RIF sont sa bande passante (pass band), sa bande de transition (transition band), sa bande rejetée (stop band) et l'atténuation dans la bande rejetée (stop band attenuation) :

En règle générale, pour Fa et Fb fixés, l'atténuation de la bande rejetée augmente avec le nombre L des coefficients du filtre.
Les coefficients du filtre peuvent être déterminés de différentes manières. Nous allons utiliser ici l'algorithme de Parks-McClellan qu'implémente la fonction MATLAB remez. Pour concevoir un filtre RIF à l'aide de cette fonction et ayant les caractéristiques décrites sur le graphe ci-dessus, il faut taper :
>> b = remez(L-1,[0 Fa Fb 0.5]*2,[1 1 0 0]);
Les arguments de la fonction sont :
- la longueur du filtre -1,
- un vecteur composé des extrémités des bandes de fréquence par paire (bande passante, bande rejetée),
- un vecteur comprenant les amplitudes désirées pour les bandes de fréquence
Remarque :
Matlab normalise la fréquence par rapport au rythme de Shannon plutôt que par rapport à la fréquence d'échantillonnage, c'est la raison pour laquelle le premier vecteur est multiplié par 2.
Le résultat de la fonction sera une réponse fréquentielle se rapprochant le plus possible de la réponse désirée.
Pour visualiser la réponse en fréquence, il suffira d'utiliser la fonction freqz :
>> freqz(b,1);
Pour convertir le filtre passe-bas b en un filtre passe-bande h, taper :
>> h = b.*exp(j*2*pi*F0*[0:L-1]);
On obtient alors la réponse fréquentielle suivante :
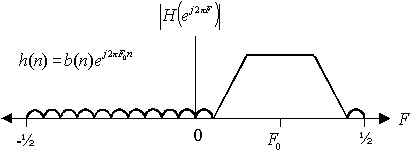
![]() Un
exemple :
Un
exemple :
Nous souhaitons concevoir un filtre passe-bande de bande passante normalisée égale à 0.1 de bande de transition égale à 0.05 centrée autour de F = 0.25. L'atténuation dans la bande rejetée devra être au moins égale à 40dB.
Il faut partir d'un filtre passe-bas avec Fa = 0.05 et Fb = 0.1.
Nous passons par les étapes suivantes :
1. Commençons par L = 20 coefficients :
>>
b = remez(19,[0 0.05 0.10 0.5]*2,[1 1 0 0]);
2. Traçons la réponse en fréquence pour vérifier si l'atténuation est suffisante :
>> freqz(b,1);
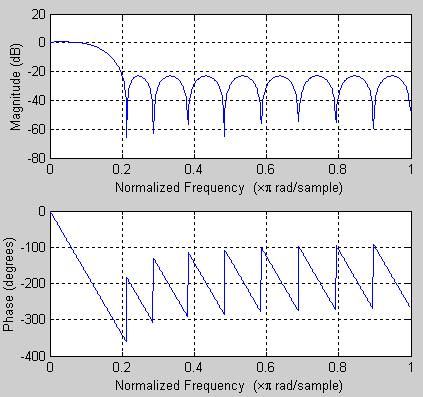
Nous constatons que l'atténuation est légèrement supérieure à 20dB, ce qui n'est pas suffisant.
3. Prenons L = 40 coefficients :
>> b = remez(39,[0 0.05 0.10 0.5]*2,[1 1 0 0]);
4. Traçons la réponse en fréquence pour vérifier si l'atténuation est suffisante :
>> freqz(b,1);
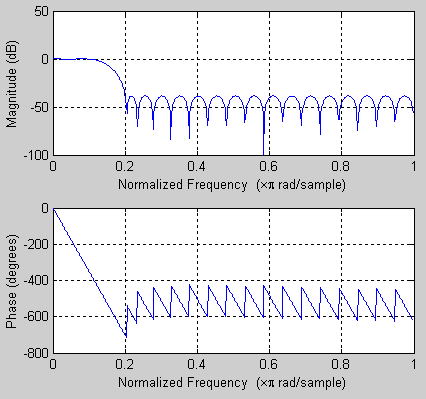
Cette fois-ci c'est bon !
5. Maintenant il faut transformer le passe-bas en passe-bande :
>> h = b.*exp(j*2*pi*0.25*[0:39]);
6. Traçons sa réponse en fréquence :
>> freqz(h,1);

Tout concorde ! Serez-vous capable
de concevoir le filtre adéquat pour la démodulation AM ?
![]()
| Ó Hervé BOEGLEN 2002 | |
| Dernières modifications le 02/03/2002 | |
| Pour toute remarque, contactez moi par email |