
Démodulation AM
Hervé BOEGLEN
![]() Cahier
des charges :
Cahier
des charges :
| modulation | AM |
| nombre de canaux | 2 |
| fréquence normalisée de la porteuse | 0.2 (canal 1), 0.3 (canal 2) |
| phase de la porteuse | inconnue |
| fichier contenant le signal d'entrée | amdat.mat |
| longueur du fichier | 10027 échantillons |
| message x(n) | bande limitée avec x(n) > 0 |
![]() Partie
1 : Démodulation non-cohérente :
Partie
1 : Démodulation non-cohérente :
Dans cette première partie, vous allez concevoir un démodulateur non cohérent dont le fonctionnement est équivalent à un détecteur d'enveloppe analogique. Sa structure est conforme au bloc-diagramme suivant :
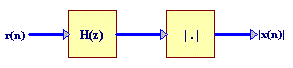
Pour le réaliser, nous aurons besoins des blocs Simulink suivants :
Simulink -> Sources -> From File
Simulink -> Discrete -> Discrete Filter
Simulink -> Math -> Abs
Le filtre H(z) doit être conçu de manière à isoler le canal désiré. Pour cela, il est intéressant de visualiser la FFT du signal d'entrée :
>> load amdat.mat
>> r = amdat(2,:);
>> N = length(r);
>> R = fft(r.*kaiser(N,5)');
>> plot(-0.5:1/N:0.5-1/N,20*log10(abs(fftshift(R))/max(abs(R))));
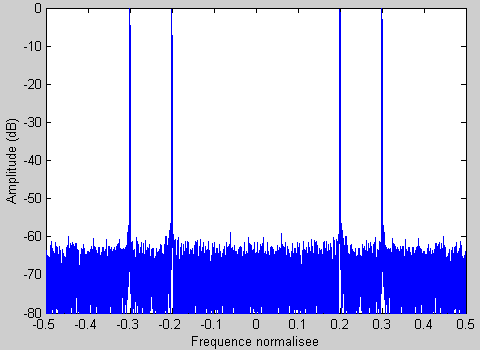
Remarquons que les pics sont centrés autour de 0.2 et 0.3 et que le plancher de bruit est situé à -60dB.
En réalité, ce ne sont pas tout à fait des pics, ce que l'on constate aisément en zoomant sur le graphe :
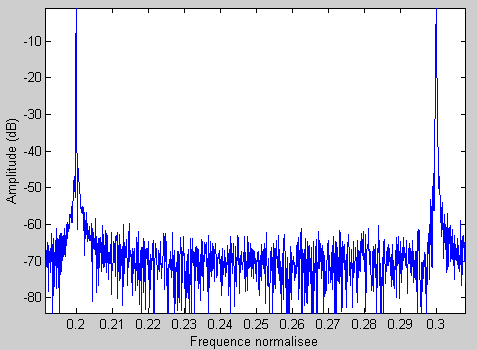
On constate que le signal centré en F1 = 0.2 possède une largeur de bande de 0.01 (c'est-à-dire qu'il s'étend de 0.195 à 0.205), autrement dit sa largeur de bande est égal à 1/100 de la fréquence d'échantillonnage.
Concevons un filtre pour isoler le canal 2 centré en F2 = 0.3. Nous allons utiliser la méthode présentée dans la page Conception de filtres FIR. On prendra une atténuation de la bande rejetée d'au moins 60dB.
Le filtre est conçu dans le workspace de MATLAB et récupéré dans le modèle SIMULINK :
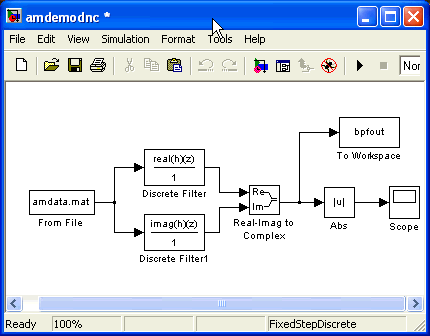
Il faut utiliser deux blocs Discrete Filter, l'un pour la partie réelle, l'autre pour la partie imaginaire.
Double-cliquer sur le premier bloc et entrer les paramètres suivants :
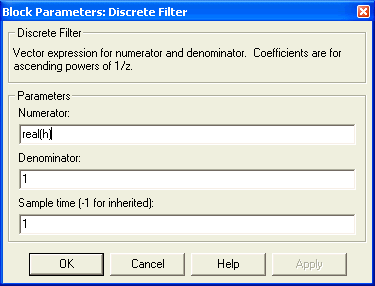
Attention ! Le signal h doit d'abord être défini sous MATLAB.
Double-cliquer sur le deuxième bloc et entrer les paramètres suivants :
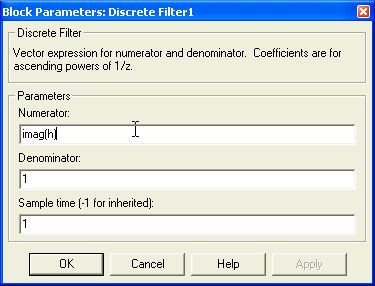
Nous avons également rajouté un bloc qui permet d'obtenir la sortie du filtre sous MATLAB. Il s'agit du bloc To Workspace que l'on trouve dans Simulink -> Sinks. Entrez les paramètres suivants :
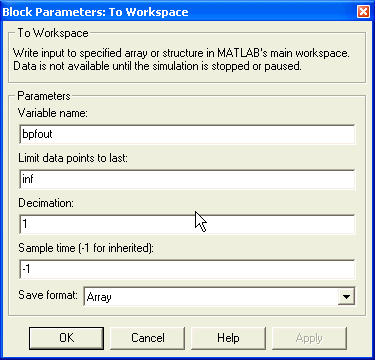
Maintenant nous sommes prêts à lancer la simulation. Sélectionner Simulation parameters... (ou CTRL+E) dans le menu Simulation et entrez les paramètres suivants :
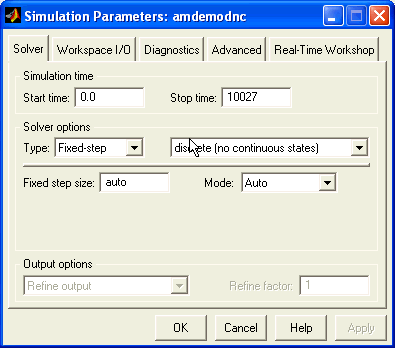
Lancer la simulation. Vous devriez obtenir ceci :
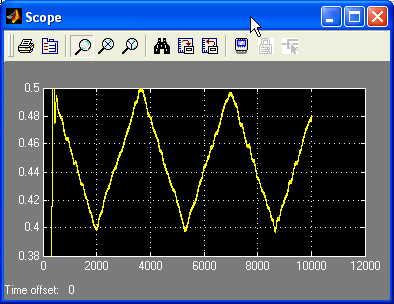
Remarque :
Vous pouvez éditer les axes X et Y du bloc Scope en cliquant dessus avec le bouton droit de la souris et en fixant manuellement les valeurs min et max.
![]() Exercice
:
Exercice
:
![]() Concevoir
un filtre passe-bande avec F1 = 0.2 et relancer la simulation pour démoduler
le canal 1.
Concevoir
un filtre passe-bande avec F1 = 0.2 et relancer la simulation pour démoduler
le canal 1.
![]() Partie
2 : Démodulation cohérente :
Partie
2 : Démodulation cohérente :
La structure est conforme au schéma-bloc suivant :
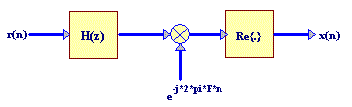
1. Utiliser le même filtre RIF que dans la partie 1.
2. Pour constituer une exponentielle complexe, vous aurez besoin de deux blocs Sine Wave et d'un bloc Real-Imag to Complex.
3. Pour sélectionner la partie réelle du signal complexe, utiliser le bloc Complex to Real-Imag. Double-cliquer sur le bloc et sélectionner Real comme paramètre de sortie.
4. Connecter ces blocs pour obtenir le schéma ci-dessous :
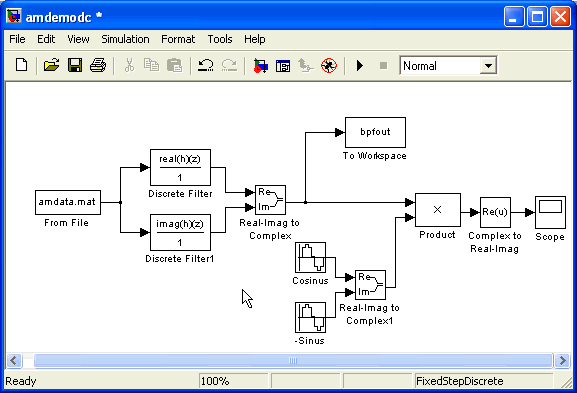
5. Double-cliquer sur le bloc Cosinus et entrer les paramètres suivants :
| Amplitude | 1 |
| Frequency (rad/sec) | 2*pi*0.3 |
| Phase (rad) | pi/2 |
| Sample time |
1
|
5. Double-cliquer sur le bloc -Sinus et entrer les paramètres suivants :
| Amplitude | -1 |
| Frequency (rad/sec) | 2*pi*0.3 |
| Phase (rad) | 0 |
| Sample time |
1
|
6. Les paramètres de simulation sont identiques à ceux de la partie 1. Lancer la simulation. Vous devriez obtenir la même chose que dans la partie 1.
![]() Exercice
:
Exercice
:
![]() Démoduler
le canal 1.
Démoduler
le canal 1.
Vous allez obtenir un signal bien plus petit que dans la partie 1. Ceci est dû au fait que l'oscillateur local à l'émission possédait un déphasage différent que celui de vous utilisez pour la démodulation (0°).
![]() Déterminer
la valeur de ce déphasage. Attention ! Le
décalage de phase entre le cosinus et le -sinus doit rester égal
à pi/2.
Déterminer
la valeur de ce déphasage. Attention ! Le
décalage de phase entre le cosinus et le -sinus doit rester égal
à pi/2.
![]()
| Ó Hervé BOEGLEN 2002 | |
| Dernières modifications le 02/03/2002 | |
| Pour toute remarque, contactez moi par email |